
 |
Search DSS Finding Data Analyzing Data Citing data About Us DSS lab consultation schedule (Monday-Friday)
*No appts. necessary during walk-in hrs. Note: the DSS lab is open as long as Firestone is open, no appointments necessary to use the lab computers for your own analysis.  
|
Home Introduction to Regression
IntroductionRegression analysis is used when you want to predict a continuous dependent variable from a number of independent variables. If the dependent variable is dichotomous, then logistic regression should be used. (If the split between the two levels of the dependent variable is close to 50-50, then both logistic and linear regression will end up giving you similar results.) The independent variables used in regression can be either continuous or dichotomous. Independent variables with more than two levels can also be used in regression analyses, but they first must be converted into variables that have only two levels. This is called dummy coding and will be discussed later. Usually, regression analysis is used with naturally-occurring variables, as opposed to experimentally manipulated variables, although you can use regression with experimentally manipulated variables. One point to keep in mind with regression analysis is that causal relationships among the variables cannot be determined. While the terminology is such that we say that X "predicts" Y, we cannot say that X "causes" Y. Number of casesWhen doing regression, the cases-to-Independent Variables (IVs) ratio should ideally be 20:1; that is 20 cases for every IV in the model. The lowest your ratio should be is 5:1 (i.e., 5 cases for every IV in the model). Accuracy of dataIf you have entered the data (rather than using an established dataset), it is a good idea to check the accuracy of the data entry. If you don't want to re-check each data point, you should at least check the minimum and maximum value for each variable to ensure that all values for each variable are "valid." For example, a variable that is measured using a 1 to 5 scale should not have a value of 8. Missing dataYou also want to look for missing data. If specific variables have a lot of missing values, you may decide not to include those variables in your analyses. If only a few cases have any missing values, then you might want to delete those cases. If there are missing values for several cases on different variables, then you probably don't want to delete those cases (because a lot of your data will be lost). If there are not too much missing data, and there does not seem to be any pattern in terms of what is missing, then you don't really need to worry. Just run your regression, and any cases that do not have values for the variables used in that regression will not be included. Although tempting, do not assume that there is no pattern; check for this. To do this, separate the dataset into two groups: those cases missing values for a certain variable, and those not missing a value for that variable. Using t-tests, you can determine if the two groups differ on other variables included in the sample. For example, you might find that the cases that are missing values for the "salary" variable are younger than those cases that have values for salary. You would want to do t-tests for each variable with a lot of missing values. If there is a systematic difference between the two groups (i.e., the group missing values vs. the group not missing values), then you would need to keep this in mind when interpreting your findings and not overgeneralize. After examining your data, you may decide that you want to replace the missing values with some other value. The easiest thing to use as the replacement value is the mean of this variable. Some statistics programs have an option within regression where you can replace the missing value with the mean. Alternatively, you may want to substitute a group mean (e.g., the mean for females) rather than the overall mean. The default option of statistics packages is to exclude cases that are missing values for any variable that is included in regression. (But that case could be included in another regression, as long as it was not missing values on any of the variables included in that analysis.) You can change this option so that your regression analysis does not exclude cases that are missing data for any variable included in the regression, but then you might have a different number of cases for each variable. OutliersYou also need to check your data for outliers (i.e., an extreme value on a particular item) An outlier is often operationally defined as a value that is at least 3 standard deviations above or below the mean. If you feel that the cases that produced the outliers are not part of the same "population" as the other cases, then you might just want to delete those cases. Alternatively, you might want to count those extreme values as "missing," but retain the case for other variables. Alternatively, you could retain the outlier, but reduce how extreme it is. Specifically, you might want to recode the value so that it is the highest (or lowest) non-outlier value. NormalityYou also want to check that your data is normally distributed. To do this, you can construct histograms and "look" at the data to see its distribution. Often the histogram will include a line that depicts what the shape would look like if the distribution were truly normal (and you can "eyeball" how much the actual distribution deviates from this line). This histogram shows that age is normally distributed:
 You can also construct a normal probability plot. In this plot, the actual scores are ranked and sorted, and an expected normal value is computed and compared with an actual normal value for each case. The expected normal value is the position a case with that rank holds in a normal distribution. The normal value is the position it holds in the actual distribution. Basically, you would like to see your actual values lining up along the diagonal that goes from lower left to upper right. This plot also shows that age is normally distributed:
 You can also test for normality within the regression analysis by looking at a plot of the "residuals." Residuals are the difference between obtained and predicted DV scores. (Residuals will be explained in more detail in a later section.) If the data are normally distributed, then residuals should be normally distributed around each predicted DV score. If the data (and the residuals) are normally distributed, the residuals scatterplot will show the majority of residuals at the center of the plot for each value of the predicted score, with some residuals trailing off symmetrically from the center. You might want to do the residual plot before graphing each variable separately because if this residuals plot looks good, then you don't need to do the separate plots. Below is a residual plot of a regression where age of patient and time (in months since diagnosis) are used to predict breast tumor size. These data are not perfectly normally distributed in that the residuals about the zero line appear slightly more spread out than those below the zero line. Nevertheless, they do appear to be fairly normally distributed.
 In addition to a graphic examination of the data, you can also statistically examine the data's normality. Specifically, statistical programs such as SPSS will calculate the skewness and kurtosis for each variable; an extreme value for either one would tell you that the data are not normally distributed. "Skewness" is a measure of how symmetrical the data are; a skewed variable is one whose mean is not in the middle of the distribution (i.e., the mean and median are quite different). "Kurtosis" has to do with how peaked the distribution is, either too peaked or too flat. "Extreme values" for skewness and kurtosis are values greater than +3 or less than -3. If any variable is not normally distributed, then you will probably want to transform it (which will be discussed in a later section). Checking for outliers will also help with the normality problem.
LinearityRegression analysis also has an assumption of linearity. Linearity means that there is a straight line relationship between the IVs and the DV. This assumption is important because regression analysis only tests for a linear relationship between the IVs and the DV. Any nonlinear relationship between the IV and DV is ignored. You can test for linearity between an IV and the DV by looking at a bivariate scatterplot (i.e., a graph with the IV on one axis and the DV on the other). If the two variables are linearly related, the scatterplot will be oval.
 Looking at the above bivariate scatterplot, you can see that friends is linearly related to happiness. Specifically, the more friends you have, the greater your level of happiness. However, you could also imagine that there could be a curvilinear relationship between friends and happiness, such that happiness increases with the number of friends to a point. Beyond that point, however, happiness declines with a larger number of friends. This is demonstrated by the graph below:
 You can also test for linearity by using the residual plots described previously. This is because if the IVs and DV are linearly related, then the relationship between the residuals and the predicted DV scores will be linear. Nonlinearity is demonstrated when most of the residuals are above the zero line on the plot at some predicted values, and below the zero line at other predicted values. In other words, the overall shape of the plot will be curved, instead of rectangular. The following is a residuals plot produced when happiness was predicted from number of friends and age. As you can see, the data are not linear:
 The following is an example of a residuals plot, again predicting happiness from friends and age. But, in this case, the data are linear:
 If your data are not linear, then you can usually make it linear by transforming IVs or the DV so that there is a linear relationship between them. Sometimes transforming one variable won't work; the IV and DV are just not linearly related. If there is a curvilinear relationship between the DV and IV, you might want to dichotomize the IV because a dichotomous variable can only have a linear relationship with another variable (if it has any relationship at all). Alternatively, if there is a curvilinear relationship between the IV and the DV, then you might need to include the square of the IV in the regression (this is also known as a quadratic regression). The failure of linearity in regression will not invalidate your analysis so much as weaken it; the linear regression coefficient cannot fully capture the extent of a curvilinear relationship. If there is both a curvilinear and a linear relationship between the IV and DV, then the regression will at least capture the linear relationship.
HomoscedasticityThe assumption of homoscedasticity is that the residuals are approximately equal for all predicted DV scores. Another way of thinking of this is that the variability in scores for your IVs is the same at all values of the DV. You can check homoscedasticity by looking at the same residuals plot talked about in the linearity and normality sections. Data are homoscedastic if the residuals plot is the same width for all values of the predicted DV. Heteroscedasticity is usually shown by a cluster of points that is wider as the values for the predicted DV get larger. Alternatively, you can check for homoscedasticity by looking at a scatterplot between each IV and the DV. As with the residuals plot, you want the cluster of points to be approximately the same width all over. The following residuals plot shows data that are fairly homoscedastic. In fact, this residuals plot shows data that meet the assumptions of homoscedasticity, linearity, and normality (because the residual plot is rectangular, with a concentration of points along the center):
 Heteroscedasiticy may occur when some variables are skewed and others are not. Thus, checking that your data are normally distributed should cut down on the problem of heteroscedasticity. Like the assumption of linearity, violation of the assumption of homoscedasticity does not invalidate your regression so much as weaken it.
Multicollinearity and SingularityMulticollinearity is a condition in which the IVs are very highly correlated (.90 or greater) and singularity is when the IVs are perfectly correlated and one IV is a combination of one or more of the other IVs. Multicollinearity and singularity can be caused by high bivariate correlations (usually of .90 or greater) or by high multivariate correlations. High bivariate correlations are easy to spot by simply running correlations among your IVs. If you do have high bivariate correlations, your problem is easily solved by deleting one of the two variables, but you should check your programming first, often this is a mistake when you created the variables. It's harder to spot high multivariate correlations. To do this, you need to calculate the SMC for each IV. SMC is the squared multiple correlation ( R2 ) of the IV when it serves as the DV which is predicted by the rest of the IVs. Tolerance, a related concept, is calculated by 1-SMC. Tolerance is the proportion of a variable's variance that is not accounted for by the other IVs in the equation. You don't need to worry too much about tolerance in that most programs will not allow a variable to enter the regression model if tolerance is too low.
Statistically, you do not want singularity or multicollinearity because
calculation of the regression coefficients is done through matrix inversion.
Consequently, if singularity exists, the inversion is impossible, and if
multicollinearity exists the inversion is unstable. Logically, you don't want
multicollinearity or singularity because if they exist, then your IVs are
redundant with one another. In such a case, one IV doesn't add any predictive
value over another IV, but you do lose a degree of freedom. As such, having
multicollinearity/ singularity can weaken your analysis. In general, you
probably wouldn't want to include two IVs that correlate with one another at .70
or greater.
As mentioned in the section above, when one or more variables are not normally distributed, you might want to transform them. You could also use transformations to correct for heteroscedasiticy, nonlinearity, and outliers. Some people do not like to do transformations because it becomes harder to interpret the analysis. Thus, if your variables are measured in "meaningful" units, such as days, you might not want to use transformations. If, however, your data are just arbitrary values on a scale, then transformations don't really make it more difficult to interpret the results. Since the goal of transformations is to normalize your data, you want to re- check for normality after you have performed your transformations. Deciding which transformation is best is often an exercise in trial-and-error where you use several transformations and see which one has the best results. "Best results" means the transformation whose distribution is most normal. The specific transformation used depends on the extent of the deviation from normality. If the distribution differs moderately from normality, a square root transformation is often the best. A log transformation is usually best if the data are more substantially non-normal. An inverse transformation should be tried for severely non-normal data. If nothing can be done to "normalize" the variable, then you might want to dichotomize the variable (as was explained in the linearity section). Direction of the deviation is also important. If the data is negatively skewed, you should "reflect" the data and then apply the transformation. To reflect a variable, create a new variable where the original value of the variable is subtracted from a constant. The constant is calculated by adding 1 to the largest value of the original variable.
If you have transformed your data, you need to keep that in mind when
interpreting your findings. For example, imagine that your original variable was
measured in days, but to make the data more normally distributed, you needed to
do an inverse transformation. Now you need to keep in mind that the higher the
value for this transformed variable, the lower the value the original variable,
days. A similar thing will come up when you "reflect" a variable. A greater
value for the original variable will translate into a smaller value for the
reflected variable.
Simple linear regression is when you want to predict values of one variable, given values of another variable. For example, you might want to predict a person's height (in inches) from his weight (in pounds). Imagine a sample of ten people for whom you know their height and weight. You could plot the values on a graph, with weight on the x axis and height on the y axis. If there were a perfect linear relationship between height and weight, then all 10 points on the graph would fit on a straight line. But, this is never the case (unless your data are rigged). If there is a (nonperfect) linear relationship between height and weight (presumably a positive one), then you would get a cluster of points on the graph which slopes upward. In other words, people who weigh a lot should be taller than those people who are of less weight. (See graph below.)
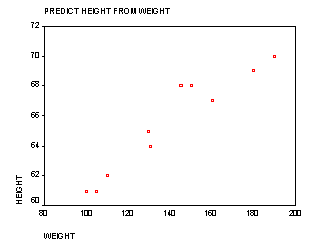
The purpose of regression analysis is to come up with an equation of a line that
fits through that cluster of points with the minimal amount of deviations from
the line. The deviation of the points from the line is called "error." Once you
have this regression equation, if you knew a person's weight, you could then
predict their height. Simple linear regression is actually the same as a
bivariate correlation between the independent and dependent variable.
Standard multiple regression is the same idea as simple linear regression, except now you have several independent variables predicting the dependent variable. To continue with the previous example, imagine that you now wanted to predict a person's height from the gender of the person and from the weight. You would use standard multiple regression in which gender and weight were the independent variables and height was the dependent variable. The resulting output would tell you a number of things. First, it would tell you how much of the variance of height was accounted for by the joint predictive power of knowing a person's weight and gender. This value is denoted by "R2". The output would also tell you if the model allows you to predict a person's height at a rate better than chance. This is denoted by the significance level of the overall F of the model. If the significance is .05 (or less), then the model is considered significant. In other words, there is only a 5 in a 100 chance (or less) that there really is not a relationship between height and weight and gender. For whatever reason, within the social sciences, a significance level of .05 is often considered the standard for what is acceptable. If the significance level is between .05 and .10, then the model is considered marginal. In other words, the model is fairly good at predicting a person's height, but there is between a 5-10% probability that there really is not a relationship between height and weight and gender. In addition to telling you the predictive value of the overall model, standard multiple regression tells you how well each independent variable predicts the dependent variable, controlling for each of the other independent variables. In our example, then, the regression would tell you how well weight predicted a person's height, controlling for gender, as well as how well gender predicted a person's height, controlling for weight. To see if weight was a "significant" predictor of height you would look at the significance level associated with weight on the printout. Again, significance levels of .05 or lower would be considered significant, and significance levels .05 and .10 would be considered marginal. Once you have determined that weight was a significant predictor of height, then you would want to more closely examine the relationship between the two variables. In other words, is the relationship positive or negative? In this example, we would expect that there would be a positive relationship. In other words, we would expect that the greater a person's weight, the greater his height. (A negative relationship would be denoted by the case in which the greater a person's weight, the shorter his height.) We can determine the direction of the relationship between weight and height by looking at the regression coefficient associated with weight. There are two kinds of regression coefficients: B (unstandardized) and beta (standardized). The B weight associated with each variable is given in terms of the units of this variable. For weight, the unit would be pounds, and for height, the unit is inches. The beta uses a standard unit that is the same for all variables in the equation. In our example, this would be a unit of measurement that would be common to weight and height. Beta weights are useful because then you can compare two variables that are measured in different units, as are height and weight. If the regression coefficient is positive, then there is a positive relationship between height and weight. If this value is negative, then there is a negative relationship between height and weight. We can more specifically determine the relationship between height and weight by looking at the beta coefficient for weight. If the beta = .35, for example, then that would mean that for one unit increase in weight, height would increase by .35 units. If the beta=-.25, then for one unit increase in weight, height would decrease by .25 units. Of course, this relationship is valid only when holding gender constant. A similar procedure would be done to see how well gender predicted height. However, because gender is a dichotomous variable, the interpretation of the printouts is slightly different. As with weight, you would check to see if gender was a significant predictor of height, controlling for weight. The difference comes when determining the exact nature of the relationship between gender and height. That is, it does not make sense to talk about the effect on height as gender increases or decreases (sex is not measured as a continuous variable). Imagine that gender had been coded as either 0 or 1, with 0 = female and 1=male. If the beta coefficient of gender were positive, this would mean that males are taller than females. If the beta coefficient of gender were negative, this would mean that males are shorter than females. Looking at the magnitude of the beta, you can more closely determine the relationship between height and gender. Imagine that the beta of gender were .25. That means that males would be .25 units taller than females. Conversely, if the beta coefficient were -.25, this would mean that males were .25 units shorter than females. Of course, this relationship would be true only when controlling for weight. As mentioned, the significance levels given for each independent variable indicates whether that particular independent variable is a significant predictor of the dependent variable, over and above the other independent variables. Because of this, an independent variable that is a significant predictor of a dependent variable in simple linear regression may not be significant in multiple regression (i.e., when other independent variables are added into the equation). This could happen because the variance that the first independent variable shares with the dependent variable could overlap with the variance that is shared between the second independent variable and the dependent variable. Consequently, the first independent variable is no longer uniquely predictive and thus would not show up as being significant in the multiple regression. Because of this, it is possible to get a highly significant R2, but have none of the independent variables be significant. Based on a document by Deborah R. Abrams
|